Description:
- Secure Hash Algorithms, also known as SHA,These algorithms are designed to be one-way functions, meaning that once they’re transformed into their respective hash values, they are almost impossible to transform back into the original data
- It works by transforming the data using a hash function
- hash function:Is an algorithm that uses bitwise operations, modular additions, and compression functions to produces a fixed-size string that can't traced back to the original
- Types of SHA available are SHA-1, SHA-2, and SHA-3, each of which was successively designed with increasingly stronger encryption in response to hacker attacks
- SHA 0 is now unusable due to the widely exposed vulnerabilities
- SHA's are commenly used to save passwords at the backend , as in to safegaurd the user passwords during an attack , as the passwords are saved as hash values ,hackers have no way of tracing back to the actual password
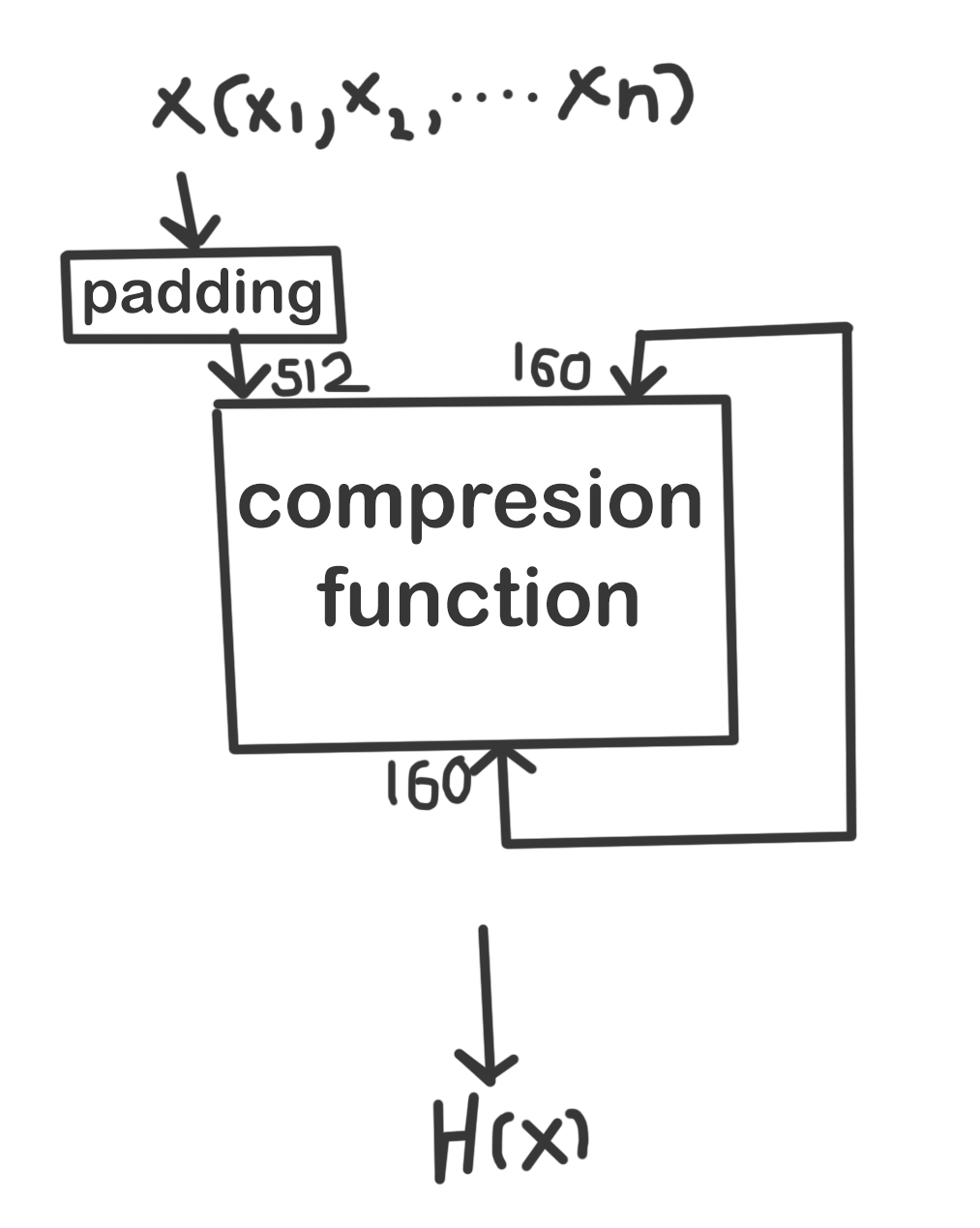
Block size: 512 Bits
No. of rounds:80
Size:160 bits
Functions used in the algorithm:
f(i;B,C,D) = (B ∧ C)∨((¬B)∧D) for 0≥i≥19
f(i;B,C,D) = B ⊕ C ⊕ D for 20≥i≥39
f(i;B,C,D) = (B ∧ C) ∨ (B ∧ D)∨ (C ∧ D) for 40≥i≥59
f(i;B,C,D) = B⊕ C ⊕ D for 60≥i≥79
constants:
K(i)=5A827999, where 0≤i≤19 round 1
K(i)=6ED9EBA1, where 20≤i≤39 round 2
K(i)=8F1BBCDC, where 40≤i≤59 round 3
K(i)=CA62C1D6, where 60≤i≤79 round 4
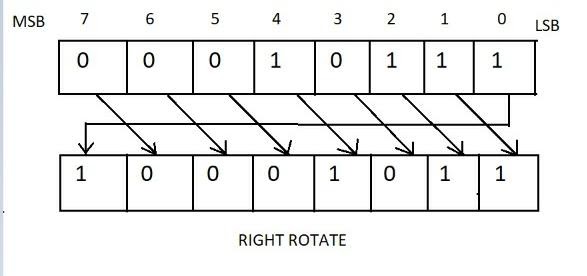
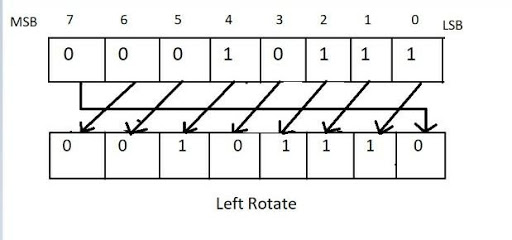
Circular shift operation(s(x,n)):
1.The left-shift operation:
when X<<n ,discard the leftmost n bits of X and padding the result with n zeroes on the right.
The right-shift operation:
when X>>32−n,discard the rightmost n bits of X and padding the result with n zeroes on the left
ALGORITHM:-
SHA-1 works by feeding a message as a bit string of length less than 2^64 bits,it produces a 160-bit hash value known as a message digest.
STEPS OF ENCRYPTION:
STEP 1:
The first step is to initialize five random strings of hex characters that will serve as part of the hash function (shown in hex):
H0 = 67DE2A01
H1 = BB03E28C
H2 = 011EF1DC
H3 = 9293E9E2
H4 = CDEF23A9
STEP 2:
In the second step padding is done, by appending(adding) a 1 at the end.
Example:
Let's Suppose the original message is the bit string:
01100111 00100110 01101011 01101100 01101100.
this gives,
01100111 00100110 01101011 01101100 01101100 1.
(67266B6C6C80 in hex).
then after appending 1 enough 0s are appended until the message is 448 bits(1
hex=4bits).
67266B6C 6C800000 00000000 00000000
00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000
00000000 00000000
The last 64 bits of the last 512-bit block are reserved for the length l of the original message.
The length of the message represented by 64 bits is then added to the end, producing a message
that is 512 bits long, it 40 length message gets stored as 28 with 0's padded ahead
67266B6C 6C800000 00000000 00000000
00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000000
00000000 00000000 00000000 00000028
now the message fits 512 bits completely as 1 hex occupies 4bits (128*4=512)
STEP 3:
The padded input obtained above, is then divided into 512-bit chunks(when message is greater than
448 bits), and each chunk is further divided into sixteen 32-bit words, W0 … W(15)
if there’s more than one chunk, each chunk gets divided in into 32bits chunks individually
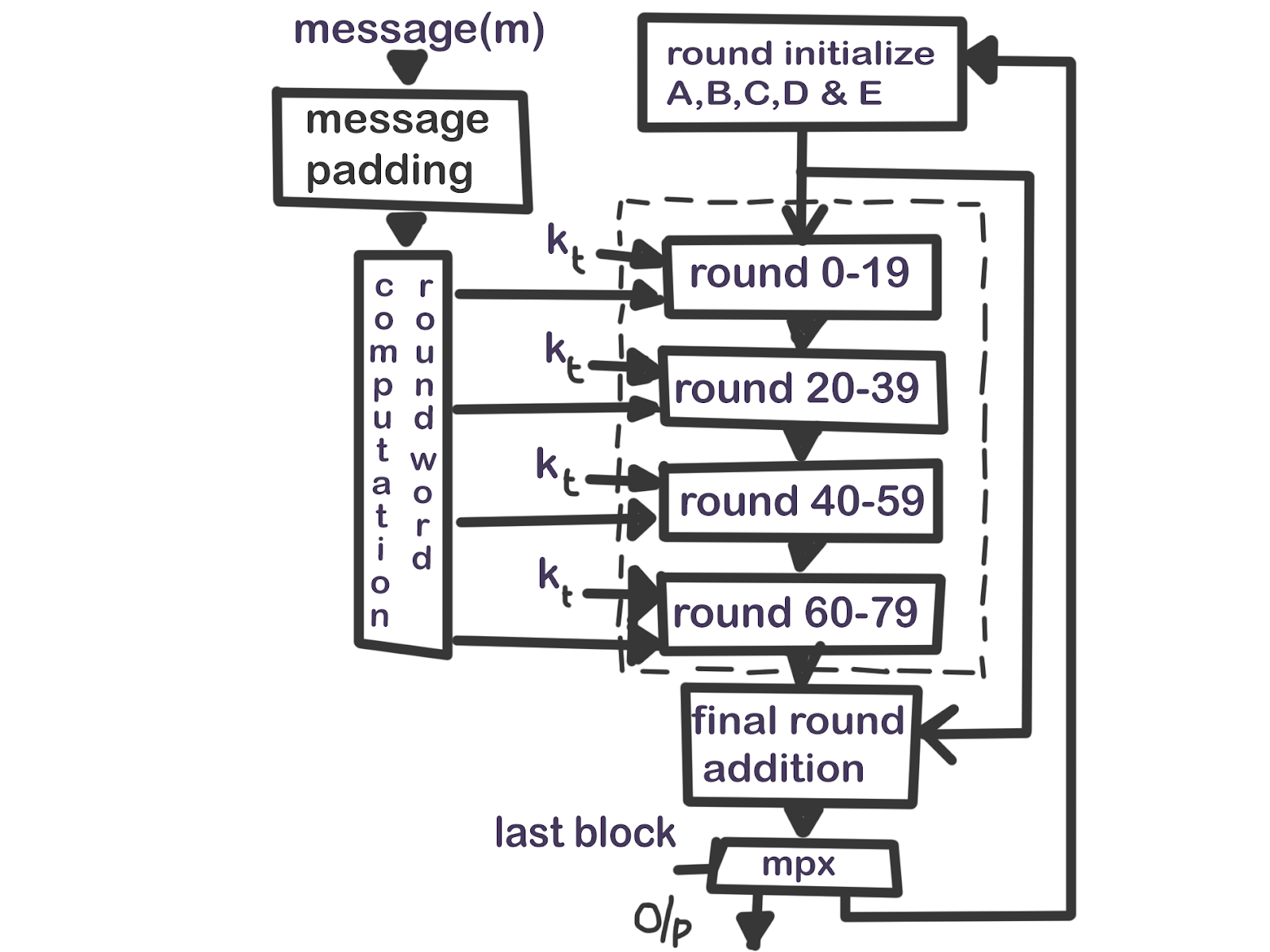
STEP: 4
For each chunk, begin the 80 iterations(rounds) necessary for hashing (80 is a predetermined
number for SHA-1), and execute the following steps on each chunk(512 bits)
The words of the 80-word sequence are labeled R(0), R(1),..., R(79). A single word buffer TEMP
is also employed
blocks(chunk 512 bits) M(1), M(2),..., M(n). The processing of each M(i) involves 80
steps(rounds).
Before processing any blocks, the H's are initialized as follows: in hex,
H0 = 67452301
H1 = EFCDAB89
H2 = 98BADCFE
H3 = 10325476
H4 = C3D2E1F0.
Now M(1), M(2), ... , M(n) are processed. To process M(i), we proceed as follows:
A) Divide M(i) into 16 words R(0), R(1), ... ,R(15), where R(0) is the left-most word.
B) For t = 16 to 79 let
W(t) = S^1(W(t-3) XOR W(t-8) XOR W(t-14) XOR W(t-16)).
C) Let A = H0, B = H1, C = H2, D = H3, E = H4. (for 1st iteration)
D) For t = 0 to 79 do,
TEMP = S^5(A) + f(t;B,C,D) + E + W(t) + K(t);
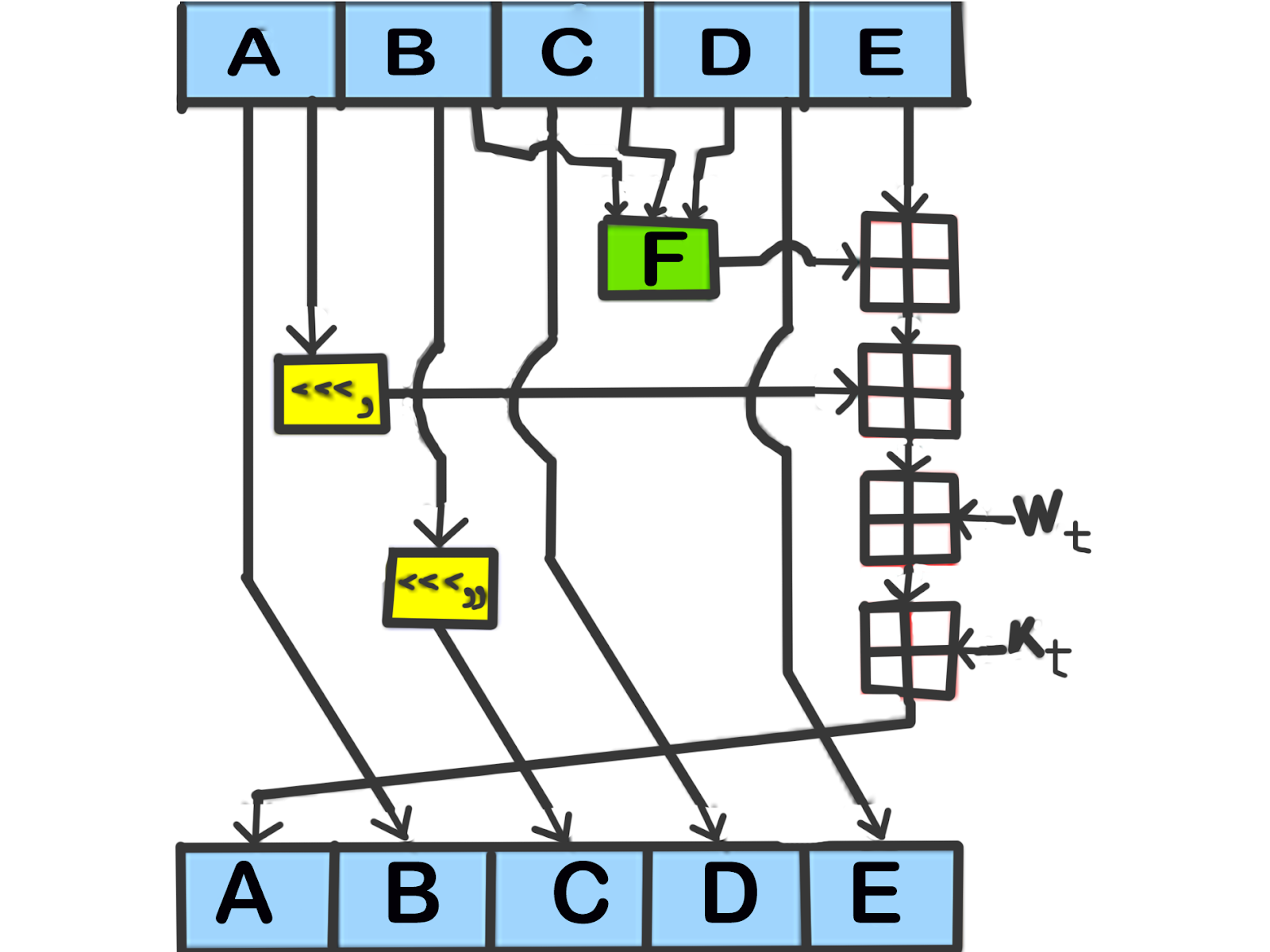
E = D; D = C; C = S^30(B); B = A; A = TEMP;
E) Let H0 = H0 + A, H1 = H1 + B, H2 = H2 + C, H3 = H3 + D, H4 = H4 + E.
After processing M(n), the message digest is the 160-bit string represented by the 5 words
H0 H1 H2 H3 H4.
PREVIOUS MAJOR ATTACKS:
1.THE SHAppening:
DESCRIPTION:
On 8 October 2015, Marc Stevens, Pierre Karpman, and Thomas Peyrin published a freestart collision attack on SHA-1's compression function that requires only 257 SHA-1 evaluations. This does not directly translate into a collision on the full SHA-1 hash function (where an attacker is not able to freely choose the initial internal state), but undermines the security claims for SHA-1. In particular, it was the first time that an attack on full SHA-1 had been demonstrated; all earlier attacks were too expensive for their authors to carry them out. The authors named this significant breakthrough in the cryptanalysis of SHA-1 The SHAppening.
The method was based on their earlier work, as well as the auxiliary paths (or boomerangs) speed-up technique from Joux and Peyrin, and using high performance/cost efficient GPU cards from NVIDIA. The collision was found on a 16-node cluster with a total of 64 graphics cards. The authors estimated that a similar collision could be found by buying US$2,000 of GPU time on EC2
The authors estimated that the cost of renting enough of EC2 CPU/GPU time to generate a full collision for SHA-1 at the time of publication was between US$75K and 120K, and noted that was well within the budget of criminal organizations, not to mention national intelligence agencies. As such, the authors recommended that SHA-1 be deprecated as quickly as possible.
2.SHAttered – first public collision:
DESCRIPTION:
On 23 February 2017, the CWI (Centrum Wiskunde & Informatica) and Google announced the SHAttered attack, in which they generated two different PDF files with the same SHA-1 hash in roughly 263.1 SHA-1 evaluations. This attack is about 100,000 times faster than brute forcing a SHA-1 collision with a birthday attack, which was estimated to take 280 SHA-1 evaluations. The attack required "the equivalent processing power of 6,500 years of single-CPU computations and 110 years of single-GPU computations".
3.Birthday-Near-Collision Attack – first practical chosen-prefix attack:
DESCRIPTION:
On 24 April 2019 a paper by Gaëtan Leurent and Thomas Peyrin presented at Eurocrypt 2019 described an enhancement to the previously best chosen-prefix attack in Merkle–Damgård–like digest functions based on Davies–Meyer block ciphers. With these improvements, this method is capable of finding chosen-prefix collisions in approximately 268 SHA-1 evaluations. This is approximately 1 billion times faster (and now usable for many targeted attacks, thanks to the possibility of choosing a prefix, for example malicious code or faked identities in signed certificates) than the previous attack's 277.1 evaluations (but without chosen prefix, which was impractical for most targeted attacks because the found collisions were almost random)[47] and is fast enough to be practical for resourceful attackers, requiring approximately $100,000 of cloud processing. This method is also capable of finding chosen-prefix collisions in the MD5 function, but at a complexity of 246.3 does not surpass the prior best available method at a theoretical level (239), though potentially at a practical level (≤249).[48][49] This attack has a memory requirement of 500+ GB.
On 5 January 2020 the authors published an improved attack.[9] In this paper they demonstrate a chosen-prefix collision attack with a complexity of 263.4, that at the time of publication would cost 45k USD per generated collision.
COMMONLY USED ATTACKS ON SHA:
Pre-image ATTACK:
One of the most common attacks seen in SHA 0&1 are the pre-image attack,
A preimage attack is against the one-way property of a hash function. In a preimage attack, a message can be determined that hashes to a given value. This could allow a password attack, where the attacker can determine a password based on the hash of the password found in a database. SHA-1 is currently resistant to preimage attack
Second-preimage ATTACK:
In a second-preimage attack, a second message can be found that hashes to the same value as a given message. This allows the attacker to create fraudulent certificates at any time, not just at the time of certificate issuance. SHA-1 is currently resistant to second-preimage attack
Collision ATTACK:
A collision attack occurs when it is possible to find two different messages that hash to the same value
Attacks against hash functions are measured against the length of time required to perform a brute-force attack, in which messages are selected at random and hashed until a collision or preimage is found
The time required to find a collision by brute force is approximately 2ⁿᐟ², where n is the bit length of the hash. To find a preimage or second-preimage by brute force, approximately 2n messages must be hashed. Thus, a hash function is weakened if a collision can be found in less time than that needed to compute 2ⁿᐟ² hashes, or if a preimage or second-preimage can be found in less time than would be needed to compute 2n hashes. For common hashes the bit length is: MD5 (128 bits), SHA-1 (160 bits) and SHA-2 (224, 256, 384, or 512 bits)
Conclusion:
The time required to perform a brute-force attack keeps getting shorter due to increases in available computing power
As such, increases in hash function lengths are necessary to maintain an acceptable margin of security. In the past, an attack threshold of 2⁶⁴ operations was considered acceptable for some uses
now the bar set at 2⁸⁰, and this will soon move up to 2¹¹².
Using the formula 2ⁿᐟ², we can see that a brute-force attack against SHA-1 would require 2⁸⁰ computations. Unfortunately, security researchers have discovered an attack strategy that requires only 2⁶¹ computations. This would make the time required to perform an attack below current standards.
The bottom line is SHA-1’s collision resistance is weak and the cost of an attack is dropping; as such, SHA-1 must be replaced with SHA-2.
SHA 2:
Due to the exposed vulnerabilities of SHA-1, cryptographers modified the algorithm to produce SHA-2, which consists of not one but two hash functions known as SHA-256 and SHA-512, using 32- and 64-bit words, respectively. There are additional truncated versions of these hash functions, known as SHA-224, SHA-384, SHA-512/224, and SHA-512/256, which can be used for either part of the algorithm.
SHA-1 and SHA-2 differ in several ways; mainly, SHA-2 produces 224- or 256-sized digests, whereas SHA-1 produces a 160-bit digest; SHA-2 can also have block sizes that contain 1024 bits, or 512 bits, like SHA-1.
Brute force attacks on SHA-2 are not as effective as they are against SHA-1. A brute force search for finding a message that corresponds to a given digest of length LL using brute force would require 2^L2 evaluations, which makes SHA-2 a lot safer against these kinds of attacks
SOURCES:
https://www.youtube.com/watch?v=YCf80-8xhGs
https://www.ipa.go.jp/security/rfc/RFC3174EN.html
https://brilliant.org/wiki/secure-hashing-algorithms/